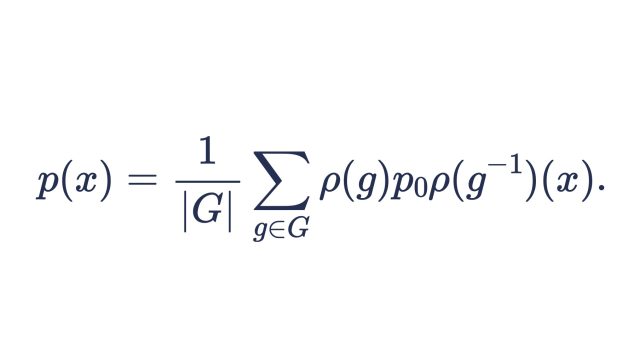1+1/4+1/9+…はどうなる？オイラーが解決したバーゼル問題の証明夜空の観測所

突然ですが、次の無限足し算の値はどうなるかわかりますか？

\[ \frac{1}{1}+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+ \cdots = \,? \]

分母はすべて平方数です。

結論を言うとこうなります：

\[ \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots = \frac{\pi^2}{6}. \]

「どうして円周率が！？」と思いますよね。

私がバーゼル問題に出会ったのは小学5年生のときですが、そのときすごく感動しました。

というわけで、この記事ではできるだけわかりやすくバーゼル問題について解説していきたいと思います。

Contents

1 バーゼル問題の経緯
2 解き方：\(\sin x\) のマクローリン展開から
3 最後に

バーゼル問題の経緯

1650年、次のような問題が数学界に投げかけられました：

\[ \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+ \cdots = \,? \]

この問題は注目を集め、名だたる数学者たちが次々と挑戦していきました。

しかし、半世紀が経ってもこの問題を解決した人は現れませんでした。

そんな中、レオンハルト・オイラーという28歳の若い数学者が1734年にこの問題を解きました。

その噂は瞬く間に広まり、オイラーが言っていることが正しいこともわかりました。

オイラーはこれをきっかけに一流の数学者として認められるようになったというわけですね。

オイラーの故郷のスイスのバーゼルにちなんで、この問題はバーゼル問題 (Basel Problem) と呼ばれています。

ここまでがわかりやすい解説で、ここから実際の解き方を解説していきます。

わからない方は雰囲気だけでも味わっていただけたらうれしいです。

解き方：\(\sin x\) のマクローリン展開から

次の式を示すのが目標である：

\[ \sum_{k=1}^{\infty} \frac{1}{k^2}=\frac{\pi^2}{6}. \]

ここで \( \sin x\) のマクローリン展開は次で与えられる：

\begin{eqnarray} \sin x &=& \sum_{k=0}^{\infty} \frac{(-1)^k x^{2k+1}}{(2k+1)!} \\ &=& x -\frac{x^3}{6} +\frac{x^5}{120} – \cdots. \end{eqnarray}

この両辺を \(x\) で割ると次の式が得られる：

\[ \frac{\sin x}{x} = 1 -\frac{x^2}{6} +\frac{x^4}{120} – \cdots. \]

(\(x=0\) のときも極限で定義すれば問題ない)

ここで、\(\dfrac{\sin x}{x}\) は \( x=\pm n\pi \) (\(n\) は自然数) で \(0\) になるから、形式的に「因数分解」ができる。

(厳密には複素解析の定理が必要だが、今は省略)

よって次のように表せる：

\begin{eqnarray} \frac{\sin x}{x} &=& \left( 1-\frac{x}{\pi} \right)\left( 1+\frac{x}{\pi} \right)\cdots \\ &=& \left (1-\frac{x^2}{\pi^2} \right) \left (1-\frac{x^2}{4\pi^2} \right) \cdots \\ &=& \prod_{k=1}^{\infty} \left(1-\frac{x^2}{k^2\pi^2} \right). \end{eqnarray}

ここで \(\dfrac{\sin x}{x}\) のマクローリン展開を思い出す：

\[ \frac{\sin x}{x} = 1 -\frac{x^2}{6} +\frac{x^4}{120} – \cdots. \]

さきほどの式と \(x\) に関する恒等式で結ばれているので係数比較が可能である。

ここで \(x^2\) の係数を比較してみる。

\( \left (1-\dfrac{x^2}{\pi^2} \right) \left (1-\dfrac{x^2}{4\pi^2} \right) \cdots \) の \(x^2\) の係数を求めたい。

この無限積はかっこの中からひとつずつ要素を取り出してかけたものの無限和として表せる。

つまり、この無限和には \( \left( -\dfrac{x^2}{\pi^2} \right) \cdot 1 \cdot 1 \cdot \cdots \) や \( 1 \cdot \left( -\dfrac{x^2}{2^2\pi^2} \right) \cdot 1 \cdot \cdots \) が含まれる。

積の係数が \(x^2\) になる組み合わせはこれらしかない。

よって \(x^2\) の係数を比較して

\[ -\frac{1}{6} = -\frac{1}{\pi^2} \sum_{k=1}^{\infty} \frac{1}{k^2}. \]

よって次が得られた：

\[ \sum_{k=1}^{\infty} \frac{1}{k^2}=\frac{\pi^2}{6}. \, \, \, \square \]