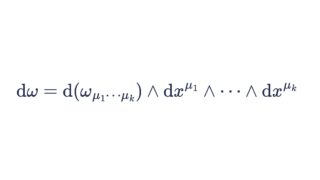「ゲージ理論」っていう名前の響き、なんかかっこいいですよね。
物理学科の人で「ゲージ理論を勉強したい!」という人もいると思います。
そこで、今回はゲージ群が \(U(1)\) という一番簡単な場合のゲージ理論を解説していきます。
この場合は電磁場が対応し、マクスウェルの方程式が得られます。
ゲージ理論は最先端物理学にも繋がっていく内容なので、これが理解できるとこれから先の理論の見通しがよくなるはずです。
できるだけわかりやすく解説したのでぜひ最後まで読んでみてください。
マクスウェル作用
物理学の理論には必ず作用が登場し、それを変分することで運動方程式を得ることができます。
今回活躍する作用はこちらです:
\[ S_{\text{Maxwell}} = \int -\frac{1}{4} F_{\mu\nu}F^{\mu\nu}-J_{\mu}A^{\mu} \, \mathrm{d}^4 x \]
添字はすべてアインシュタインの縮約記法で書かれています。
添字を上げ下げするのに使う計量はミンコフスキー計量で、\(\eta_{\mu\nu}=\eta^{\mu\nu}=\text{diag}( -1,1,1,1) \) とします。
なので添字は \(\mu=0,1,2,3, \, \nu=0,1,2,3\) とします。
\(x^0=t\) で、\( (x^1,x^2,x^3) = (x,y,z) \) を表すと思ってもらえればわかりやすいでしょう。
ここで \(\phi\) をスカラーポテンシャル、\(\boldsymbol{A}\) をベクトルポテンシャルとして
\[ (A_\mu)=\left(\phi, -\boldsymbol{A} \right) \]
とし、\(\boldsymbol{J}\) を電流密度ベクトルとして
\[ (J_\mu)=( -\rho, \boldsymbol{J}) \]
とします。
\(\mu\) はあくまで添え字です。
成分を明示して書けば
\[ (A_0, A_1, A_2, A_3)=\left(\phi, -A_x, -A_y, -A_z \right) \]
と
\[ (J_0, J_1, J_2, J_3)=( -\rho, J_x, J_y, J_z) \]
です。
今回は面倒を避けるため \(c=1\) とした単位系を使っています。
単位を合わせるのは後でがんばりましょう笑
また、ゲージ場を \(A_{\mu}\) として
\[ A^{\mu}=\eta^{\mu\nu}A_{\nu}, \, F_{\mu\nu}=\partial_\mu A_{\nu}-\partial_\nu A_\mu, \, F^{\mu\nu}=\eta^{\mu\rho}\eta^{\nu\sigma}F_{\rho\sigma}\]
です。
ちなみに \(A_{\mu}\) は本来は純虚数に値を取る \(1\)-形式で、 \(A=A_{\mu} \mathrm{d} x^{\mu} \) を外微分すると
\begin{eqnarray}
\mathrm{d} A&=& \mathrm{d} A_{\mu} \wedge \mathrm{d} x^{\mu} \\
&=& \partial_{\nu} A_{\mu} \mathrm{d} x^{\nu} \wedge \mathrm{d} x^{\mu} \\
&=& (\partial_0 A_1-\partial_1 A_0) \mathrm{d} x^0 \wedge \mathrm{d} x^1+(\partial_0 A_2-\partial_2 A_0) \mathrm{d} x^0 \wedge \mathrm{d} x^2+(\partial_0 A_3-\partial_3 A_0) \mathrm{d} x^0 \wedge \mathrm{d} x^3+(\partial_1 A_2-\partial_2 A_1) \mathrm{d} x^1 \wedge \mathrm{d} x^2+(\partial_1 A_3-\partial_3 A_1) \mathrm{d} x^1 \wedge \mathrm{d} x^3+(\partial_2 A_3-\partial_3 A_2) \mathrm{d} x^2 \wedge \mathrm{d} x^3 \\
&=& (\partial_\mu A_\nu-\partial_\nu A_\mu) \mathrm{d} x^\mu \wedge \mathrm{d} x^\nu \\
&=& F_{\mu\nu} \mathrm{d} x^{\mu} \wedge \mathrm{d} x^{\nu}
\end{eqnarray}
なので \(F=\mathrm{d}A\) です。
外微分について詳しくは以下の記事をどうぞ↓
この性質が後で大活躍します。
どうしてこんなややこしい設定をしたのかはヤン・ミルズ理論を勉強すればわかると思いますが、今回は省略します。
目的はこの作用からマクスウェルの方程式4本を導くことです:
- ガウスの法則 \(\nabla \cdot \boldsymbol{E}=\rho \)
- アンペール・マクスウェルの法則 \(\nabla \times \boldsymbol{B}-\partial_t \boldsymbol{E}=\boldsymbol{J}\)
- 磁束保存の法則 \(\nabla \cdot \boldsymbol{B}=0\)
- ファラデーの電磁誘導の法則 \(\nabla \times \boldsymbol{E}+\partial_t \boldsymbol{B}=0\)
それではさっそくやってみましょう。
マクスウェル作用の変分
マクスウェル作用は以下で与えられる:
\[ S_{\text{Maxwell}} = \int -\frac{1}{4} F_{\mu\nu}F^{\mu\nu}-J_{\mu}A^{\mu} \, \mathrm{d}^4 x. \]
これを変分する。
ゲージ場 \(A_\mu\) で変分すると、計量や電流密度ベクトルの変分は \(0\) になるから
\begin{eqnarray}
\delta S_{\text{Maxwell}} &=& \int -\frac{1}{4} \delta(F_{\mu\nu}F^{\mu\nu})-\delta(J_{\mu}A^{\mu}) \, \mathrm{d}^4 x \\
&=& \int -\frac{1}{4} \delta F_{\mu\nu} \cdot F^{\mu\nu}-\frac{1}{4} F_{\mu\nu} \cdot \delta F^{\mu\nu}-\delta J_{\mu} \cdot A^{\mu}-J_{\mu} \cdot \delta A^{\mu} \, \mathrm{d}^4 x \\
&=& \int -\frac{1}{4} \delta F_{\mu\nu} \cdot F^{\mu\nu}-\frac{1}{4} F_{\mu\nu}\eta^{\mu\rho} \eta^{\nu\sigma} \delta F_{\rho\sigma}-J_{\mu} \cdot \delta A^{\mu} \, \mathrm{d}^4 x \\
&=& \int -\frac{1}{2} F^{\mu\nu}\delta F_{\mu\nu}-J_{\mu} \cdot \delta A^{\mu} \, \mathrm{d}^4 x \\
&=& \int -\frac{1}{2} F^{\mu\nu}(\partial_\mu \delta A_\nu -\partial_\nu \delta A_\mu)-J_{\mu} \cdot \delta A^{\mu} \, \mathrm{d}^4 x \\
&=& \int -\frac{1}{2} F^{\mu\nu}\partial_\mu \delta A_\nu -\frac{1}{2} F^{\nu\mu}\partial_\nu \delta A_\mu-J_{\mu} \cdot \delta A^{\mu} \, \mathrm{d}^4 x \\
&=& \int – F^{\mu\nu}\partial_\mu \delta A_\nu -J_{\mu} \cdot \delta A^{\mu} \, \mathrm{d}^4 x. \\
\end{eqnarray}
6番目の式変形では \(F^{\mu\nu}=-F^{\nu\mu}\) を使った。
ここで \(-F^{\mu\nu}\partial_\mu \delta A_\nu\) の \(A_\nu\) にかかっている微分が邪魔なので部分積分すると、境界項は消えて
\begin{eqnarray}
&=& \int -F^{\mu\nu}\partial_\mu \delta A_\nu -J_{\mu} \cdot \delta A^{\mu} \, \mathrm{d}^4 x \\
&=& \int \partial_\mu F^{\mu\nu}\delta A_\nu -J_{\mu} \cdot \delta A^{\mu} \, \mathrm{d}^4 x \\
&=& \int \partial_\mu F^{\mu\nu}\delta A_\nu -J^{\nu} \cdot \delta A_{\nu} \, \mathrm{d}^4 x \\
&=& \int (\partial_\mu F^{\mu\nu} -J^{\nu})\delta A_\nu \, \mathrm{d}^4 x. \\
\end{eqnarray}
ここで、任意の \(\delta A_\nu\) に対して \(\delta S_{\text{Maxwell}}=0\) が成立することが条件なので次の方程式を得る:
\[\partial_\mu F^{\mu\nu} =J^{\nu}.\]
曲率を求める
ここで、今まで \(F^{\mu\nu}\) の具体的な成分を求めていなかった。
電場と磁場のポテンシャルによる式を思い出す:
\[ \boldsymbol{E}=-\nabla \phi-\partial_t \boldsymbol{A} \]
および
\[ \boldsymbol{B}=-\nabla \times \boldsymbol{A}. \]
よって次を得る:
\begin{eqnarray}
(F_{\mu \nu}) &=& (\partial_{\mu}A_{\nu}-\partial_{\nu}A_{\mu}) \\
&=& \begin{pmatrix} 0 & E_{x} & E_{y} & E_{z} \\\ -E_{x} & 0 & -B_{z} & B_{y} \\ -E_{y} & B_{z} & 0 & -B_{x} \\ -E_{z} & -B_{y} & B_{x} & 0 \end{pmatrix}.
\end{eqnarray}
ここから \(F^{\mu\nu}=\eta^{\mu\rho}\eta^{\nu\sigma}F_{\rho\sigma}\) を計算すると
\[ (F^{\mu \nu})= \begin{pmatrix} 0 & -E_{x} & -E_{y} & -E_{z} \\\ E_{x} & 0 & -B_{z} & B_{y} \\ E_{y} & B_{z} & 0 & -B_{x} \\ E_{z} & -B_{y} & B_{x} & 0 \end{pmatrix}. \]
これでようやく次の方程式が使える:
\[\partial_\mu F^{\mu\nu} =J^{\nu}.\]
ガウスの法則を導く
次の定義を思い出そう:
\[ (J^\mu)=( \rho, \boldsymbol{J}). \]
よって、方程式
\[\partial_\mu F^{\mu\nu} =J^{\nu}\]
で \(\nu=0\) とすると
\[ \frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}=\rho. \]
これは \(\nabla \cdot \boldsymbol{E}=\rho\) に他ならない。
アンペール・マクスウェルの法則を導く
方程式
\[\partial_\mu F^{\mu\nu} =J^{\nu}.\]
で \(\nu=1,2,3\) とする。
\(\nu=1\) では
\[ -\frac{\partial E_x}{\partial t}+\frac{\partial B_z}{\partial y}-\frac{\partial B_y}{\partial z}=J_x. \]
\(\nu=2\) では
\[ -\frac{\partial E_y}{\partial t}-\frac{\partial B_z}{\partial x}+\frac{\partial B_x}{\partial z}=J_y. \]
\(\nu=3\) では
\[ -\frac{\partial E_z}{\partial t}+\frac{\partial B_y}{\partial x}-\frac{\partial B_x}{\partial y}=J_z. \]
これらをベクトルとしてまとめると \(\nabla \times \boldsymbol{B}-\partial_t \boldsymbol{E}=\boldsymbol{J}\) になる。
磁束保存の法則を導く
変分から出る方程式は上記の2つのみである。
残りはビアンキの恒等式を使わなければならない。
今回は \(F=\mathrm{d}A\) だったので、\(\mathrm{d}F=\mathrm{d}^2 A=0\) となる。
\(\mathrm{d}^2=0\) は外微分の有名な性質。
(詳しくはこちらの記事で↓)
よって、\(2\)-形式を \(F=F_{\mu\nu} \mathrm{d} x^\mu \wedge \mathrm{d} x^\nu\) とすると \(\mathrm{d}F=0.\)
添字が4つしかないから手計算してしまおう。
\begin{eqnarray}
\mathrm{d}F &=& \mathrm{d}F_{\mu\nu} \wedge \mathrm{d} x^\mu \wedge \mathrm{d} x^\nu \\
&=& \partial_\rho F_{\mu\nu} \mathrm{d} x^\rho \wedge \mathrm{d} x^\mu \wedge \mathrm{d} x^\nu \\
&=& (\partial_0 F_{12}-\partial_0 F_{21}-\partial_1 F_{02}+\partial_1 F_{20}+\partial_2 F_{01}-\partial_2 F_{10}) \mathrm{d} x^0 \wedge \mathrm{d} x^1 \wedge \mathrm{d} x^2+(\partial_0 F_{13}-\partial_0 F_{31}-\partial_1 F_{03}+\partial_1 F_{30}+\partial_3 F_{01}-\partial_3 F_{10}) \mathrm{d} x^0 \wedge \mathrm{d} x^1 \wedge \mathrm{d} x^3+(\partial_0 F_{23}-\partial_0 F_{32}-\partial_2 F_{03}+\partial_2 F_{30}+\partial_3 F_{02}-\partial_3 F_{20}) \mathrm{d} x^0 \wedge \mathrm{d} x^2 \wedge \mathrm{d} x^3+(\partial_1 F_{23}-\partial_1 F_{32}-\partial_2 F_{13}+\partial_2 F_{31}+\partial_3 F_{12}-\partial_3 F_{21}) \mathrm{d} x^1 \wedge \mathrm{d} x^2 \wedge \mathrm{d} x^3 \\
&=& 0.
\end{eqnarray}
よってこの微分形式の成分はすべて \(0\) になる。
まずは \(\mathrm{d} x^1 \wedge \mathrm{d} x^2 \wedge \mathrm{d} x^3\) の係数を見ると
\[ \partial_1 F_{23}-\partial_1 F_{32}-\partial_2 F_{13}+\partial_2 F_{31}+\partial_3 F_{12}-\partial_3 F_{21}=0\]
が得られた。
これを置き換えると
\[ -2\frac{\partial B_x}{\partial x}-2\frac{\partial B_y}{\partial y}-2\frac{\partial B_z}{\partial z}=0. \]
よって \(\nabla \cdot \boldsymbol{B}=0\) を得る。
ファラデーの電磁誘導の法則を導く
先ほどの微分形式にはまだ係数が残っている。
\( \mathrm{d} x^0 \wedge \mathrm{d} x^2 \wedge \mathrm{d} x^3 \) の係数は \(x\) に、\( \mathrm{d} x^0 \wedge \mathrm{d} x^1 \wedge \mathrm{d} x^3 \) の係数は \(y\) に、\( \mathrm{d} x^0 \wedge \mathrm{d} x^1 \wedge \mathrm{d} x^2 \) の係数は \(z\) に対応する。
それらの係数すべてが \(0\) であるから、計算すると \(\nabla \times \boldsymbol{E}+\partial_t \boldsymbol{B}=0\) を得る。
最後に
一苦労でしたが、なんとかマクスウェルの方程式4本を導くことができました。
これが \(U(1)\) のゲージ理論です。
\(U(1)\) は可換群だったので計算が楽でしたが、\(SU(2)\) はやばいみたいです。
私がさらに勉強して理解できたら、いずれ紹介するかもしれません。
物理学は面白いですね。
気に入ってもらえたならうれしいです。
では。
参考にした書籍↓