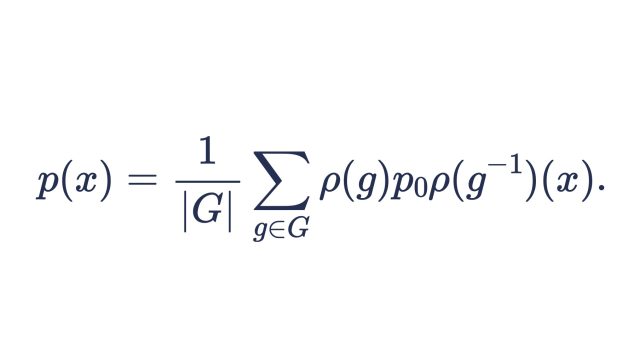望遠鏡和とは？級数を求める問題で大活躍！公式や具体例も紹介夜空の観測所

みなさんは「望遠鏡和」という言葉を知っていますか？

簡単に言うと「プラスとマイナスがバサバサ消えていって和が簡単に求められる」というやつで、高校数学でも大活躍するやつです。

ですが「プラスとマイナスがバサバサ消える」という和について今まで専門用語がなかったみたいです。

そこでせきゅーんさん(関真一朗さん)が「望遠鏡和」という用語を考え出しました。

私もかなり昔からせきゅーんさんのブログを読んでいて、「望遠鏡和って名前かっこいいな…」と思っていました。

そこで今回、望遠鏡和がどんなものなのかをわかりやすく解説していこうと思います。

Contents

1 望遠鏡和とは？
2 差分とは？
3 難しい具体例
4 望遠鏡和が使えない例
5 最後に

望遠鏡和とは？

望遠鏡和とは、簡単に言うとこんな感じです：

\begin{eqnarray} &&\left(1-\frac{1}{2} \right)+\left(\frac{1}{2}-\frac{1}{3} \right)+\cdots+\left(\frac{1}{n-1}-\frac{1}{n} \right)\\ &=&1+\left(-\frac{1}{2}+\frac{1}{2} \right)+\cdots+\left(-\frac{1}{n-1}+\frac{1}{n-1} \right)-\frac{1}{n} \\ &=& 1-\frac{1}{n}. \end{eqnarray}

プラスとマイナスがうまくバサバサ消えていって、最終的に初項と末項だけが残る仕組みです。

一般化するとこんな感じでしょう：

\[ \sum_{k=1}^n (a_{k+1}-a_k)=a_{n+1}-a_1. \]

途中のプラスとマイナスはバサバサ消えていって、最初と最後しか残りません。

つまり、求める和を \(a_{k+1}-a_k\) の形にうまく持っていければ簡単に計算できるということです。

ひとつ有名な例を紹介しましょう。

問題

\(\displaystyle \sum_{k=1}^n \frac{1}{k(k+1)} \) を求めよ。

解答

\(\dfrac{1}{k(k+1)}\) を部分分数分解すると \(\displaystyle \left(\frac{1}{k}-\frac{1}{k+1}\right) \) になる。

これは望遠鏡和の形そのものだから

\[ \sum_{k=1}^{n} \left( \frac{1}{k}-\frac{1}{k+1} \right) = 1-\frac{1}{n+1}. \, \, \, \square \]

このように、分数の和の計算では部分分数分解が活躍します。

差分とは？

ここで便利な記号を導入します。

それが差分です。

定義はこちら：

定義

前進差分 \(\Delta_k\) を次で定義する：

\[ \Delta_k (a_k) := a_{k+1}-a_k.\]

これを使うと望遠鏡和の公式がすっきりまとまりますね：

\[ \sum_{k=1}^n \Delta_k (a_k) = a_{n+1}-a_1.\]

逆に次の関係も得られます：

\[ \Delta_k \sum_{i=1}^k a_i =a_{k+1}.\]

証明は簡単で、

\begin{eqnarray} \Delta_k \sum_{i=1}^k a_i &=& \sum_{i=1}^{k+1} a_i -\sum_{i=1}^k a_i \\ &=& (a_1+ \cdots + a_{k+1}) -(a_1+\cdots+a_k) \\ &=& a_{k+1}. \end{eqnarray}

これは何かに似てませんか？

そう、微分と積分の関係です。

特に次の公式は高校数学でも有名ですね：

\[ \frac{\mathrm{d}}{\mathrm{d}x} \int_a^x f(t) \mathrm{d}t = f(x). \]

つまり、シグマと差分は互いに逆の関係にあると言えるのです。

難しい積分をするときも \(F'(t)=f(t)\) という原始関数が見つかれば勝ちだったように、難しい級数では望遠鏡和の形を見つければ勝ちなんです。

というわけで実際に難しい例を計算してみましょう。

難しい具体例

試しにこれを解いてみましょう：

問題

\( \displaystyle \sum_{k=1}^{n} \frac{k}{2^{k}} \) を求めよ。

解答

\( \dfrac{k}{2^{k}}\) を望遠鏡和に分解することを目指す。

試しにこの数列を差分してみると、

\begin{eqnarray} \Delta_k \left( \frac{k}{2^{k}} \right) &=& \frac{k+1}{2^{k+1}} -\frac{k}{2^{k}} \\ &=& \frac{k+1}{2^{k+1}} -\frac{2k}{2^{k+1}} \\ &=& \frac{1-k}{2^{k+1}}. \end{eqnarray}

\( \dfrac{k}{2^k}\) の形の気配が出てきた。

\(\Delta_k \left( \dfrac{1}{2^{k}} \right)= -\dfrac{1}{2^{k+1}} \) より、上手くまとめると

\begin{eqnarray} \Delta_k \left( \frac{-k-1}{2^{k-1}} \right) &=& \frac{-k-2}{2^{k}} -\frac{-k-1}{2^{k-1}} \\ &=& \frac{-k-2}{2^{k}} + \frac{2k+2}{2^{k}} \\ &=& \frac{k}{2^{k}}. \end{eqnarray}

よって \( \Delta_k \left( \dfrac{-k-1}{2^{k-1}} \right) = \dfrac{k}{2^{k}} \) を得る。

これが求めていた「原始関数」である。

よってこれを望遠鏡和の公式に当てはめると、

\begin{eqnarray} \sum_{k=1}^{n} \frac{k}{2^{k}} &=& \sum_{k=1}^{n} \Delta_k \left( \frac{-k-1}{2^{k-1}} \right) \\ &=& \frac{-n-2}{2^{n}} -\frac{-2}{2^{0}} \\ &=& 2 – \frac{n+2}{2^{n}}. \, \, \, \square \end{eqnarray}

答えが正しく求まりました。

積分のときの原始関数を求めるのと同じような感じですよね。

かなり便利なテクニックなので、複雑な級数に会ったら使ってみてください。

問題

\( \displaystyle \sum_{k=1}^{\infty} \frac{k}{2^{k}} \) を求めよ。

解答

\begin{eqnarray} \sum_{k=1}^{\infty} \frac{k}{2^{k}} &=& \lim_{n \to \infty} \sum_{k=1}^{n} \frac{k}{2^{k}} \\ &=& \lim_{n \to \infty} 2 -\frac{n+2}{2^{n}} \\ &=& 2. \, \, \, \square \end{eqnarray}

望遠鏡和がはまると気持ちいいですね。

また、挑戦してみたい方向けに問題を用意しておきます。

答えは記事の最後に書いたので挑戦してみてください。

問題

\( \displaystyle \sum_{k=1}^{\infty} \frac{k^2}{2^{k}} \) を求めよ。

望遠鏡和が使えない例

ただ、何でもかんでも望遠鏡和が使えるとは限りません。

例えば \( \displaystyle \sum_{k=1}^n \frac{1}{k^2} \) です。

この場合、\( a_{k+1}-a_k = \dfrac{1}{k^2} \) を満たすような数列 \(a_k\) はなかなか見つかりません。

「原始関数」が見つからない限り、望遠鏡和は威力を発揮できません。

なので別の方法を考える必要があります。

ちなみに、この級数の無限バージョンはバーゼル問題と呼ばれていてこうなります：

\[ \sum_{k=1}^{\infty} \frac{1}{k^2}=\frac{\pi^2}{6}. \]

詳しいことはこちらの記事をどうぞ。

最後に

今回は望遠鏡和について紹介しました。

望遠鏡和は名前がかっこいいだけでなく、和と差分の関係にまで迫る奥深い概念だったんです。

高校数学の難しい問題もほとんどは望遠鏡和で片付くでしょう。

難しい問題に出会ったら、ぜひ望遠鏡和を使ってみてください。

ここから問題の解説に入ります↓

問題

\( \displaystyle \sum_{k=1}^{\infty} \frac{k^2}{2^{k}} \) を求めよ。

解答

\( \dfrac{k^2}{2^{k}} \) の「原始関数」を見つけるのが目標である。

つまり、 \(a_{k+1}-a_{k}=\dfrac{k^2}{2^{k}}\) となるような \(a_{k}\) を見つけたい。

\(a_k=\dfrac{Ak^2+Bk+C}{2^{k-1}}\) と仮定すると、満たすべき恒等式は

\[ A(k+1)^2+B(k+1)+C-2(Ak^2+Bk+C)=k^2. \]

両辺を係数比較して \( (A,B,C)=( -1, -2, -3) \) を得る。

実際、

\begin{eqnarray} \Delta_k \left( \frac{-k^2-2k-3}{2^{k-1}} \right) &=& \frac{-(k+1)^2-2(k+1)-3+2k^2+4k+6}{2^{k}} \\ &=& \frac{k^2}{2^{k}}. \end{eqnarray}

これより

\begin{eqnarray} \sum_{k=1}^{n} \frac{k^2}{2^{k}} &=& \sum_{k=1}^{n} \Delta_k \left( \frac{-k^2-2k-3}{2^{k-1}} \right) \\ &=& \frac{-(n+1)^2-2(n+1)-3}{2^{n}}-\frac{-6}{2^{0}} \\ &=& 6 – \frac{n^2+4n+6}{2^{n}}. \end{eqnarray}

極限を取って

\[ \sum_{k=1}^{\infty} \frac{k^2}{2^{k}}= 6. \, \, \, \square \]

ここまで楽しんでもらえたならうれしいです。

では。

私が数学好きになったきっかけの本↓